Peta Karnaungt dan Maxterm & Minterm

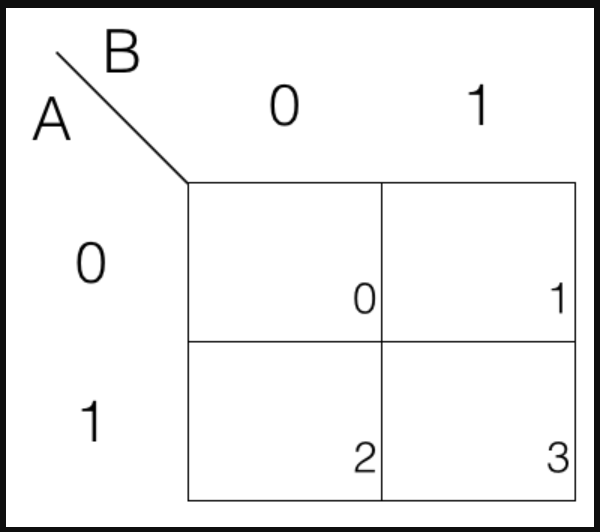
 Peta Karnaungt (K-Map)

    K-Map atau Karnaugh Map adalah representasi grafis dari kondisi input yang mirip dengan tabel kebenaran. Ini adalah array sel yang membantu dalam penyederhanaan logis atau minimalisasi ekspresi Boolean.

    Peta Karnaugh adalah representasi grafis dua dimensi dari kondisi input dan output yang dapat meminimalkan ekspresi Boolean yang melibatkan 2, 3, 4 dan 5 variabel. Dengan kata lain, ini digunakan untuk menghapus operasi yang berlebihan dalam fungsi Boolean. Ini dinamai Maurice Karnaugh, seorang matematikawan dan fisikawan Amerika, yang mengembangkan K- Map di Harvard Computation Laboratory.

Gambar 1. Maurice Karnaugh, Pendiri Peta Karnaugh

    contoh Peta Karnaugh dengan dua variabel dan setiap kotak disebut 'sel'. Empat sel diberi nomor (0, 1, 2, 3). K-Map yang memiliki n-variabel memiliki 2n sel di mana di setiap sel sesuai dengan nilai tabel kebenaran. Sel ditetapkan dengan nilai yang sesuai dengan baris tabel kebenaran. Sel-sel diatur sedemikian rupa sehingga sel-sel yang berdekatan hanya berbeda dengan satu posisi bit.

Gambar 2. Contoh Peta Karnaugh (K-Map)

Maxterm & Minterm

Maxterm

    Maxterm dari variabel 'n' adalah jumlah variabel 'n' yang muncul tepat sekali dalam bentuk True atau Complemented.

Contoh: Maxterm dari 3 variabel (X,Y,Z)= Setiap Maxterm = 0 hanya untuk satu kombinasi nilai dari variabel yang diwakilinya sebaliknya nilainya adalah 1. Oleh karena itu fungsi Boolean dapat diekspresikan secara aljabar dari tabel kebenaran yang diberikan dengan mengidentifikasi produk logis dari semua Maxterms yang menghasilkan 0 dalam fungsi tersebut. Ungkapan ini disebut sebagai Product of Maxterms atau Product-of-Sums (POS).

Gambar 3. Maxterms untuk Tiga Variabel

Minterm

    Minterm dari variabel 'n' adalah produk dari variabel 'n' yang muncul tepat sekali dalam bentuk True atau Complemented.

Contoh: Minterm dari 3 variabel(X,Y,Z) = Setiap Minterm = 1 hanya untuk satu kombinasi nilai variabel yang diwakilinya sebaliknya 0. Mengidentifikasi Minterm dari K-map sama dengan membaca persamaan dalam bentuk Sum-of-Minterms atau Sum-of-Products (SOP), langsung dari tabel kebenaran.

Gambar 4. Minterm untuk Tiga Variabel

Penyederhanaan Ekspresi Boolean Menggunakan K-Map (Peta Karnaugh)

Penyederhanaan ekspresi Boolean menggunakan K- Map membutuhkan pengelompokan 1. Pengelompokan 1 harus mengikuti aturan tertentu:

• Grup harus memiliki 2, 4, 8 satu (1).
• Identifikasi Minterms atau Maxterms diperlukan.
• Pengelompokan dilakukan secara horizontal, vertikal tetapi tidak pernah secara diagonal.
• Beberapa grup menggunakan 1 berulang dapat dilakukan.
• 
  

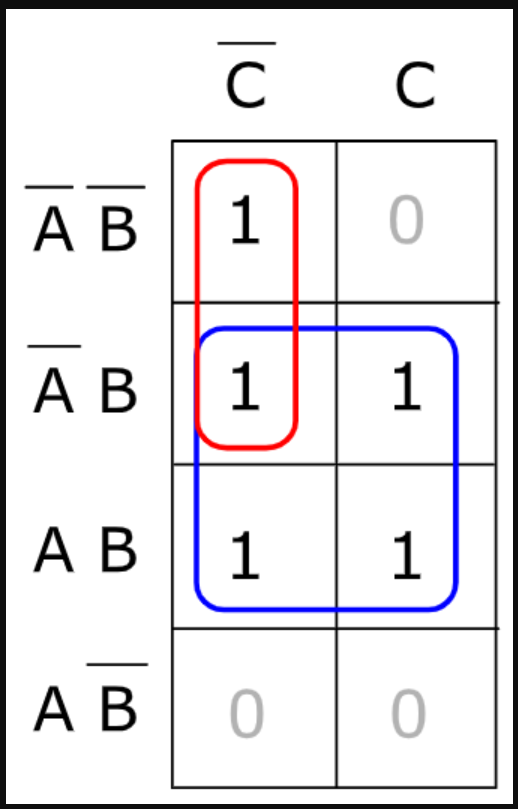
Hal ini dapat dijelaskan dengan lebih baik dengan contoh menggunakan 3 variabel seperti yang ditunjukkan di bawah ini:

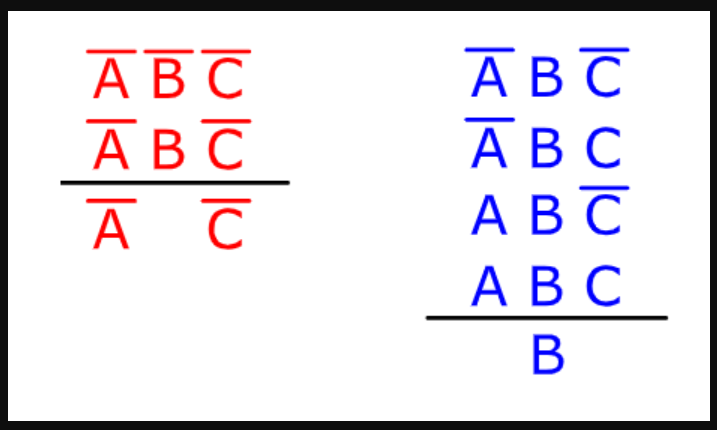
Dua kelompok terbentuk: Kelompok 1 ditandai dengan Warna Biru dan kelompok lainnya dalam Warna Merah. Grup-grup tersebut tercantum di bawah ini.

Variabel yang tersisa adalah OR'ed (Logical Addition) untuk mendapatkan ekspresi Boolean yang dikurangi.

Aplikasi dari Peta Karnaugh (K-Map)

Aplikasi tersebut meliputi:

• Mereka digunakan dalam desain dan implementasi Sirkuit Digital
• K- Maps digunakan dalam penyederhanaan sirkuit Half- Adder dan Full- Adder

Keuntungan dari K-Map

Keuntungannya meliputi:

• Sirkuit yang paling ekonomis dan disederhanakan dapat dibangun menggunakan K-Maps.
• Menggunakan K-Maps, operasi logis cepat.
• Menurunkan pada ekspresi paling sederhana membantu dalam pengurangan instruksi dalam aplikasi perangkat lunak.
• Ini lebih efisien daripada teknik penyederhanaan aljabar Boolean lainnya.

Kekurangan K-Map

K-Maps bergantung pada variabel dalam suatu ekspresi dan karenanya proses penyederhanaan menjadi kompleks dengan peningkatan variabel.